Как правильно вычислить площадь участка в форме треугольника — подробное объяснение с примерами и формулой

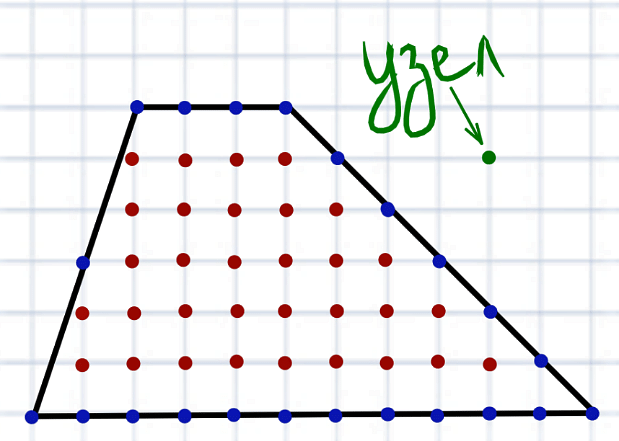
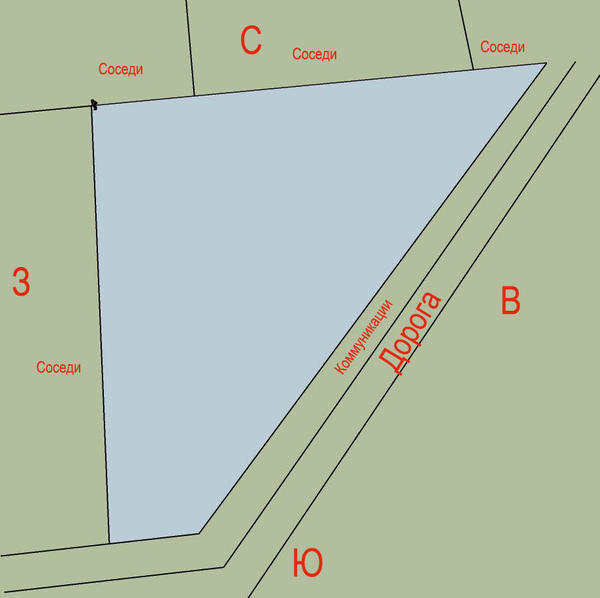
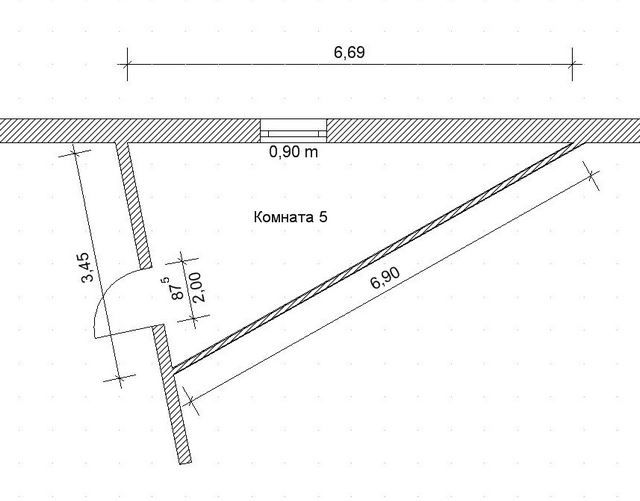
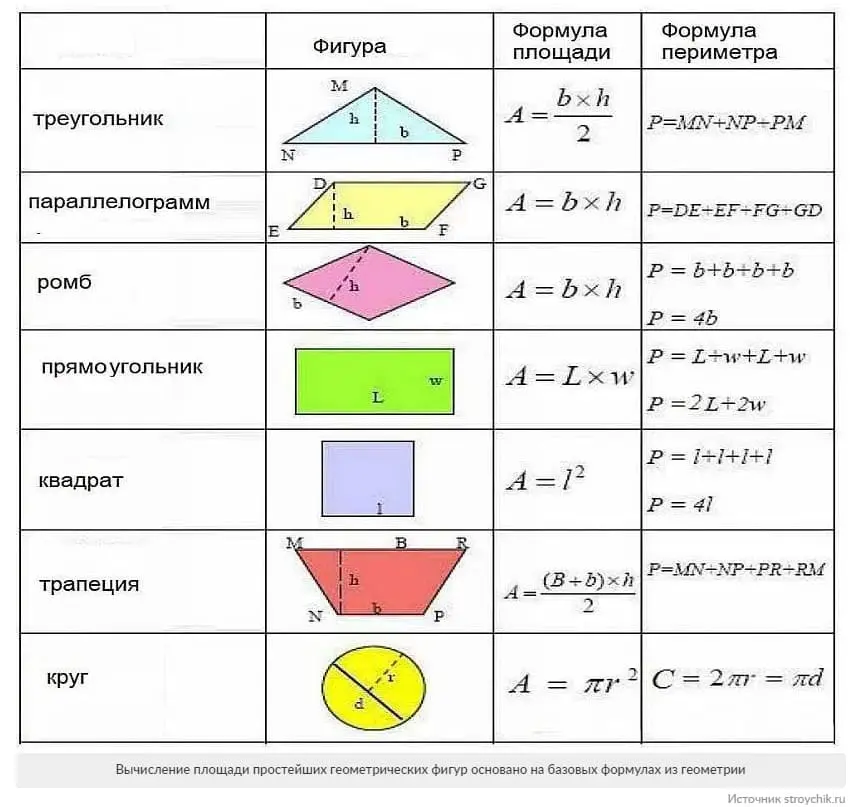
Если вы владеете участком земли, чья форма отличается от обычных прямоугольников или квадратов, то вам может понадобиться узнать его площадь. Зная площадь участка, вы сможете правильно планировать строительство, размещение сада или расчет суммы налога на собственность. В этой статье мы рассмотрим способы вычисления площади треугольного участка. Треугольники — одни из наиболее распространенных форм в природе, и их площадь может быть необъективной для неопытных пользователей.

Вычисление площади треугольника — это простой и в то же время увлекательный математический балет. Для того чтобы получить окончательный результат, вам понадобятся некоторые основные данные: длины сторон вашего треугольника или длина одной стороны и высота, опущенная из этой стороны. Если у вас нет лишних данных, не беспокойтесь, мы расскажем вам о методах вычисления площади треугольника с разными известными данными.

Подготовив все необходимые данные и вооружившись формулами, вы сможете вычислить площадь вашего треугольного участка легко и с минимальным числом ошибок. При этом помните, что вычисление площади треугольника — лишь один из множества методов определения площади необычных форм. Всякий раз, когда вам потребуется этот навык, вы сможете применить полученные знания и получить точный результат.

Раздел: Трикутники та їх площа

Для розрахунку площі треугольника, ми використовуємо базову формулу, яка базується на довжинах його сторін і висоті, опущеній з одного з вершин на протилежну сторону. Цей метод називається «половинний добуток двох сторін на сінус відповідного кута».

Отже, площа треугольника (S) може бути обчислена за допомогою формули:

S = (a * b * sin(C)) / 2

де a і b – довжини сторін треугольника, С – величина (радіани) кута між цими сторонами.

Определение основных параметров треугольника

Перед тем, как рассчитать площадь участка треугольной формы, необходимо определить основные параметры самого треугольника. Эти параметры включают длины его сторон, значения углов и высоту. Рассмотрим каждый из этих параметров подробнее.

Длины сторон: треугольник состоит из трех сторон, и каждая из них имеет свою длину. Длина сторон может быть выражена в любых единицах измерения длины, например, в метрах или футах.

Углы: треугольник имеет три угла, обозначаемых как A, B и C. Углы могут быть выражены в градусах или радианах.

Высота: высота треугольника — это отрезок, опущенный из вершины треугольника на основание или на противоположную сторону. Она может быть выражена в тех же единицах измерения длины, что и стороны.

Нахождение длин сторон

Прежде чем рассчитывать площадь участка треугольной формы, важно определить длины его сторон. Знание длин сторон поможет нам использовать соответствующую формулу для вычисления площади треугольника.

Существует несколько способов определить длину сторон треугольника. Один из самых распространенных способов — использование геометрической формулы расстояния между двумя точками на плоскости. Если известны координаты вершин треугольника, мы можем использовать эту формулу для нахождения длины каждой стороны треугольника.

Еще одним способом определения длин сторон является использование геодезических инструментов, таких как ленты, трассиры или лазерные измерители. С их помощью можно точно измерить расстояние между разными точками участка треугольной формы.

Определение длин сторон треугольника — важный шаг в рассчете площади участка. В следующих разделах мы рассмотрим различные методы рассчета площади треугольника и применим их на основе известных длин сторон.

Нахождение угла между сторонами

В треугольниках различной формы и размеров для вычисления площади участка необходимо знать значения всех трёх сторон. Однако, в некоторых случаях, при известных значениях двух сторон и угла между ними, возможно найти площадь треугольника без необходимости измерения третьей стороны.

Для нахождения угла между сторонами треугольника можно использовать одну из нескольких формул, которые основываются на тригонометрических функциях. Одной из наиболее распространенных является формула косинусов:

Формула	Значение
cos(A) = (b^2 + c^2 — a^2) / (2 * b * c)	Угол между сторонами a и b
cos(B) = (a^2 + c^2 — b^2) / (2 * a * c)	Угол между сторонами a и c
cos(C) = (a^2 + b^2 — c^2) / (2 * a * b)	Угол между сторонами b и c

Подставив известные значения двух сторон и используя соответствующую формулу, можно вычислить значение угла между этими сторонами. Затем полученное значение угла можно использовать для дальнейшего расчета площади треугольника.

Формула для измерения площади треугольника

Площадь треугольника – это важный параметр, который позволяет определить размеры и форму этой геометрической фигуры. Изучение формулы для расчета площади треугольника помогает понять ключевые концепции в геометрии и вычислительной математике.

В общем случае площадь треугольника может быть найдена как половина произведения длины основания на высоту, проходящую к этому основанию. Формула для расчета площади треугольника универсальна и позволяет вычислить площадь треугольника любой формы и размера, если известны значения основания и соответствующей высоты.

Использование формулы полупериметра и радиуса вписанной окружности

Для определения площади участка треугольной формы можно использовать формулу, основанную на понятиях полупериметра и радиуса вписанной окружности.

Полупериметр треугольника – это половина суммы длин его сторон. Он обозначается как p. Полупериметр позволяет нам определить радиус вписанной окружности по формуле r = S/p, где S – площадь треугольника.

Используя найденное значение радиуса вписанной окружности, мы можем рассчитать площадь участка треугольной формы, используя формулу S = πr², где π – математическая константа, приближенное значение которой равно 3.14159.

Видео:

Как посчитать площадь многоугольника за 15 секунд в уме? Формула для ленивых